Slimegirl Physics

A slimegirl is a mythical creature made of slime that can morph her body into any shape she likes.

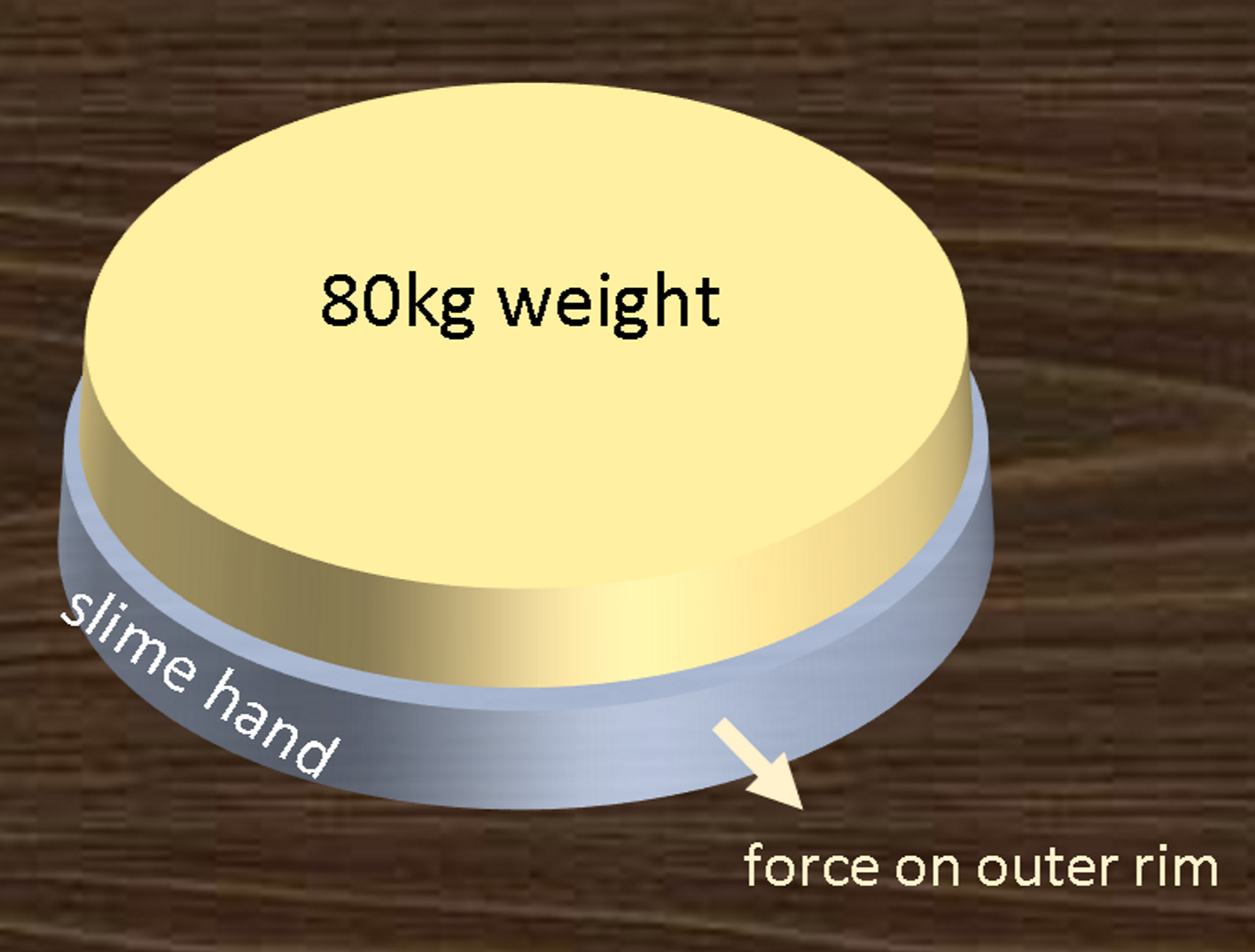
Lets assume that a slimegirl morphs her hand into a perfect disk of height 2cm, radius 5cm, density of water.

This gives the flat side of the disk an area of 78.5cm^2, which gives it a shape roughly comparable to a human palm (average surface area of human palm ~75cm^21).

Lets say this hand can withstand 80kg before it gets squished (~the mass of an average healthy male). This means that the outer rim of the disk (area 62.8cm^2) needs to be able to withstand the corresponding pressure.

The mass of this hand would be 0.157kg, negligible compared to the applied mass, and is thus ignored.

Therefore the estimated pressure that a slimegirl can withstand before getting squished is (80kg*9.8Nkg^1 / 62.8cm^-2) ≈ 12.5N cm^-2

What would be the implications?

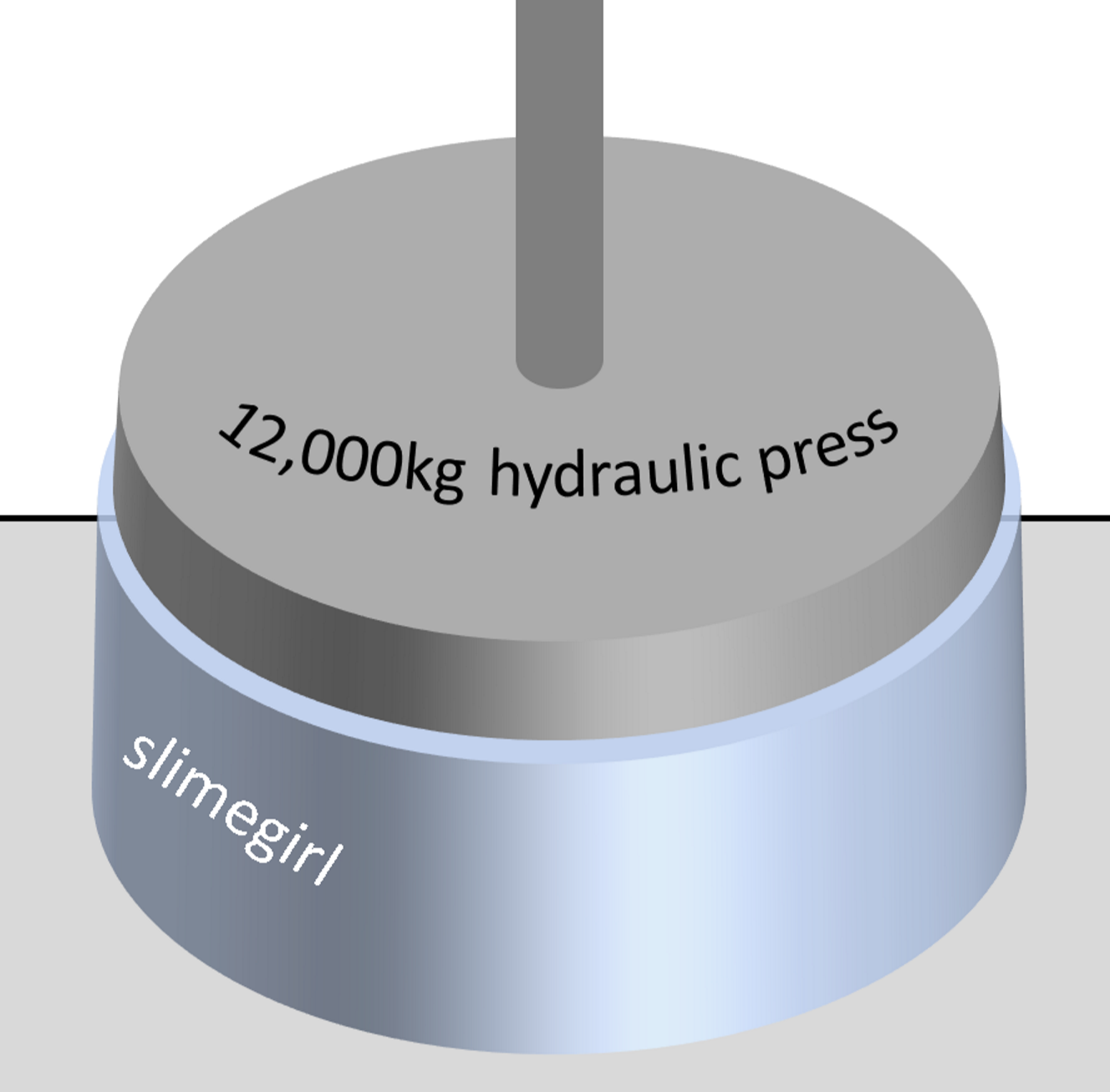
If a slimegirl of 70kg, volume 70,000cm^3, were to morph into a large disk of height 100cm, she would have an outer rim of 9380cm^2 (0.938m^2) and could thus withstand ≈ 117,000 N ≈ 12,000 kg!

For reference, a bowling ball can withstand around 10,000kg2.

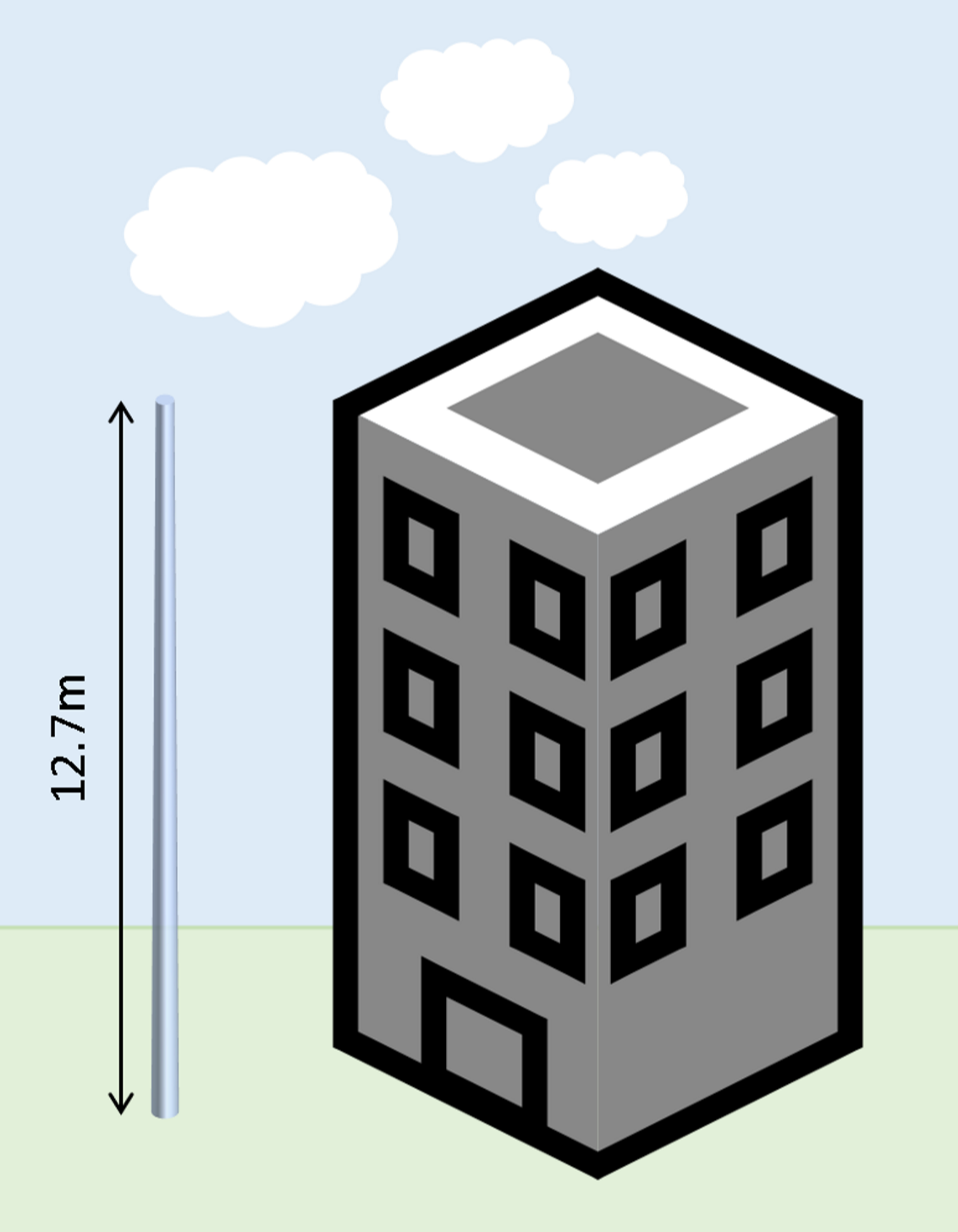
Alternatively, the tallest column a slimegirl could form before the internal pressure would become so great that she collapsed (ρgh=12.5Ncm^−2) would be 12.7 m with a radius of 4.19 cm, about the same height as a 4 story building.

It is important to note that if a slimegirl is cut or squished her body is able to reform back into its original shape, so she remains unharmed :)

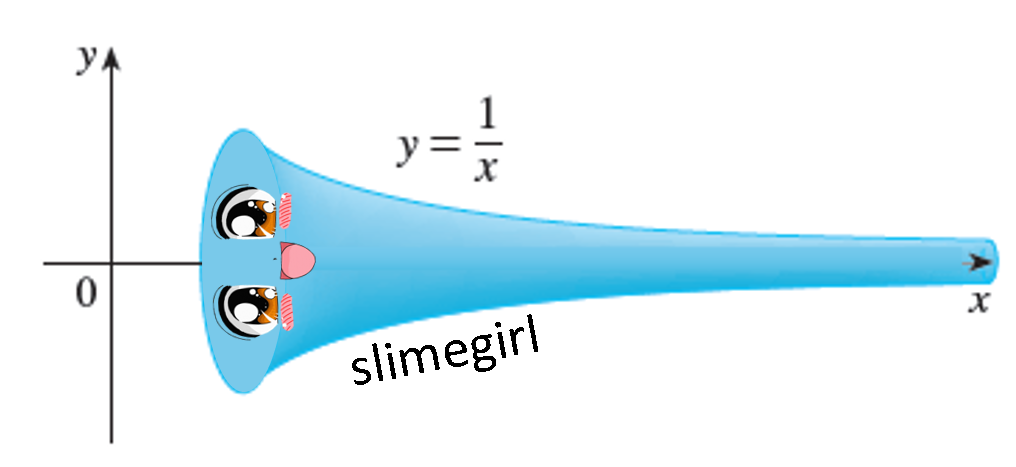
If a slimegirl were to assume a shape similar to a scaled graph of 1/x {x: x ≥ 1}, her volume would be:

as expected.

However, her area would be (where k is the scaling constant that is required to make her volume correct):

So her area would become infinite!

Truly the slimegirl is amazing.

Notes